The information leakage exists in decomposition method
Published:
This is an argument on the decomposition method (e.g., ITD, EMD) in time series forecasting.
类似EMD的信号分解方法用于预测前的预处理是否存在原理上问题
很多学者利用种种信号分解方法来分解信号后，再进行时间序列预测，常用方法有EMD（Empirical Mode Decomposition）与 ITD (Intrinsic Time-Scale Decomposition)等。 问题： 但是最近对于信号分解应用于时间序列预测的方法是否存在信息泄露问题有不同的见解,也有一些朋友遇到了类似的问题：
因此在下文中展开陈述
为何ITD与EMD等信号分解方法不适合时间序列的预测，并且以ITD为例进行公式探究。
// 本文仅陈述自己的观点，本人能力有限，如有不当请指正。//
时间序列预测的本质：
是利用历史数据对未来数据的一个猜测与估计，但是 EMD与ITD等方法在分解信号时，利用到了未来的数据对历史数据进行分解，因此存在一个信息泄露问题。
[Example]
以ITD 原文链接为例，在对 \(Χ_t\) 信号分解的时候，提取出baseline 信号 \(L_t\) 与 residual信号 \(H_t\), 其中 : \(X_t =L_t +H_t\)
\[L_{t}=L_{k}+\left(\frac{L_{k+1}-L_{k}}{X_{k+1}-X_{k}}\right)\left(S_{t}-X_{k}\right), \quad t \in\left(\tau_{k}, \tau_{k+1}\right]\] \[L_{k+1}=\alpha\left[X_{k}+\left(\frac{\tau_{k+1}-\tau_{k}}{\tau_{k+2}-\tau_{k}}\right)\left(X_{k+2}-X_{k}\right)\right]+(1-\alpha) X_{k+1}\]其中，\(τ_k\) 代表第 \(k\) 个极值对应的横坐标。那么可以看出，如果要分解时间在第 \(（τ_k，τ_{k+1}）\) 之间的信号，必须要使用到 \(τ_{k+2}\) 的信息，也就是未来的信息。
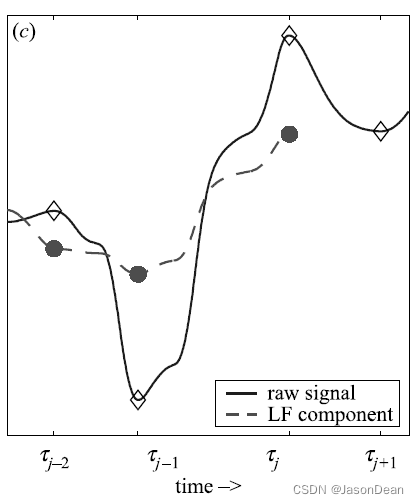
如果从图形中解释，如上图所示，当获得了 \(τ_{j+1}\) 这个点的数值 (实线)后，才能分解得到 \(τ_j\) 以及其之前的数据 (虚线)。
自己对ITD存在信息泄露的理解
如果从图形中解释，如上图所示，当获得了 \(τ_{j+1}\) 这个点的数值 (实线)后，才能分解得到 \(τ_j\) 以及其之前的数据 (虚线)。
这与时间序列预测的本质有所违背，不适合先ITD分解，后训练+预测。
- EMD与ITD类似，均需要提取未来的局部最值
- ITD对于该问题仅仅出现在窗口边缘，而EMD的问题可以清晰的体现整个窗口。
参考文献
[1] Frei Mark G and Osorio Ivan (2007), Intrinsic time-scale decomposition: time–frequency–energy analysis and real-time filtering of non-stationary signals, Proc. R. Soc. A.463321–342 http://doi.org/10.1098/rspa.2006.1761